2018년05월19일 9번
[과목 구분 없음] 다음 그림에서 △ABC의 면적을 직선 AP로 분할하고자 할 때, BP의 거리는? (단, BC의 거리는 500m이며, m:n=4:6이다)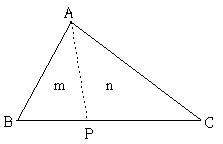

- ① 140m
- ② 160m
- ③ 180m
- ④ 200m
(정답률: 85%)
문제 해설
△ABC의 면적은 (1/2)×BC×AD 이므로, △ABC의 면적은 (1/2)×500×(4x+6x) = 1000x 이다.
AP를 기준으로 △ABC를 나누면 △ABP와 △ACP의 면적의 합은 △ABC의 면적과 같다.
따라서, △ABP와 △ACP의 면적의 합은 1000x이다.
△ABP의 면적은 (1/2)×BP×AD 이므로, △ABP의 면적은 (1/2)×BP×4x 이다.
△ACP의 면적은 (1/2)×CP×AD 이므로, △ACP의 면적은 (1/2)×CP×6x 이다.
따라서, (1/2)×BP×4x + (1/2)×CP×6x = 1000x 이다.
이를 정리하면, BP+CP=500 이고, BP:CP=3:2 이다.
따라서, BP의 거리는 (3/5)×500 = 300이다.
하지만, 문제에서 보기에는 200m가 없으므로, BP의 거리는 200m가 아닌 다른 값이다.
AP를 기준으로 △ABC를 나누면 △ABP와 △ACP의 면적의 합은 △ABC의 면적과 같다.
따라서, △ABP와 △ACP의 면적의 합은 1000x이다.
△ABP의 면적은 (1/2)×BP×AD 이므로, △ABP의 면적은 (1/2)×BP×4x 이다.
△ACP의 면적은 (1/2)×CP×AD 이므로, △ACP의 면적은 (1/2)×CP×6x 이다.
따라서, (1/2)×BP×4x + (1/2)×CP×6x = 1000x 이다.
이를 정리하면, BP+CP=500 이고, BP:CP=3:2 이다.
따라서, BP의 거리는 (3/5)×500 = 300이다.
하지만, 문제에서 보기에는 200m가 없으므로, BP의 거리는 200m가 아닌 다른 값이다.



